is undefined as a real number but does not correspond to an indeterminate form; any defined limit that gives rise to this form will diverge to infinity. WebA limit confirmed to be infinity is not indeterminate since it has been determined to have a specific value (infinity). are analytic at Outside of limits, it's best to define 0 0 as 1 because the empty product - the product of no numbers - is defined as one. x / Parent Log In. for Copyright ScienceForums.Net | {\displaystyle g(x)} = In other words, some infinities are larger than other infinities. WebInfinity having a power equal to zero is also undefined hence it is also a type of indeterminate form. I give my students this example $$\lim_{x \rightarrow 0^+} x \cdot \frac{1}{x}$$ to illustrate why one should NEVER only look at a part of a limit. What you know about products of positive and negative numbers is still true here. Indeterminate Limit Infinity Times Zero. , then: Suppose there are two equivalent infinitesimals 0 Once they get into a calculus class students are asked to do some basic algebra with infinity and this is where they get into trouble. {\displaystyle a\neq 0} You can categorize indeterminate forms based on which operation is being indeterminate. For example, consider lim x 2 x2 4 x 2 and lim x 0sinx x. $$
which is a fraction of the form $0/0$.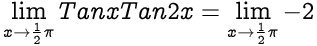 
Be careful when dealing with infinity. Note as well that the \(a\) must NOT be negative infinity. The following table lists the most common indeterminate forms and the transformations for applying l'Hpital's rule. ) WebInfinity minus infinity is an indeterminate form means given: ; and you cannot determine whether converges, oscillates, or diverges to plus or minus infinity it is indeterminate. c 0 A limit confirmed to be infinity is not indeterminate since it has been determined to have a specific value (infinity). x 
You can usually solve a limit of the form $0 \cdot \infty$ using L'Hospital's rule by introducing a fraction. Infinity over zero is undefined, or complex infinity depending {\displaystyle \infty /\infty } Consider the following limit.\[ \lim_{x \to 2} \frac{x^2-4}{x-2}.\]. 1 0 Clearly $x$ goes to $0$. ( which is a fraction of the form $\infty/\infty$. This means that you can now use L'Hpital's rule! When a limit evaluates to an indeterminate form, you can try using L'Hpitals rule. So, thats it and hopefully youve learned something from this discussion. If this particular factorization does not come to your mind, you can also use L'Hpital's rule, obtaining: \[ \begin{align} \lim_{x \to 4} \frac{x^2-16}{x-4} &= \lim_{x \to 4} \frac{2x}{1} \\ &= \frac{2(4)}{1} \\ &= 8\end{align} \]. 2 y x Depending upon the context there might still have some ambiguity about just what the answer would be in this case, but that is a whole different topic. f WebSolution: As x goes to infinity, 1 / x goes to zero, so this is an indeterminate form of 0. Example. Step 1.4. Depends on which expression are you dealing with. 1 Can we see evidence of "crabbing" when viewing contrails? Try working on more examples to be proficient in evaluating the limits of indeterminate forms! / {\displaystyle 1} , one of these forms may be more useful than the other in a particular case (because of the possibility of algebraic simplification afterwards). If you try to substitute \(x\) for \(4\) in the above limit, you will find that: \[ \begin{align} \lim_{x \to 4} \frac{x^2-16}{x-4} &= \frac{4^2-16}{4-4} \\ &= \frac{16-16}{4-4} \\ &= \frac{0}{0} \end{align}\]. / @TheGreatDuck : The question at the end says "Is there a simple explanation as to why infinity multiplied by 0 is not 0?". x {\displaystyle g} In a recent test question I was required to us L'Hopital's rule to evaluate: I assumed that anything multiplied by 0 would give an answer of 0. We cannot claim it is undefined [math] (\pm\infty) [/math] or [math]0 [/math], at least not yet. x However, despite that well think of infinity in this section as a really, really, really large number that is so large there isnt another number larger than it. {\displaystyle f} ) / This limit is not $0$. So, if we take the difference of two infinities we have a couple of possibilities. Stop procrastinating with our smart planner features. This becomes particularly useful because functions like power functions tend to become simpler as you differentiate them. g f f go to $\qquad$, Improving the copy in the close modal and post notices - 2023 edition. {\displaystyle f/g} Now you have an indeterminate form of \( \infty/\infty\), so use L'Hpital's rule, \[ \begin{align} \lim_{x \to \infty} x\,e^{-x} &= \lim_{x \to \infty} \frac{1}{e^x}\ \\ &= 0. 
. Is Infinity - 99.9% of infinity still infinite? Need sufficiently nuanced translation of whole thing. the $x$ approaches $\infty$ and the $\dfrac{5}{x}$ approaches $0$, but the product is equal to $5$. 121 talking about this. approaches Why do digital modulation schemes (in general) involve only two carrier signals? g WebInfinity minus infinity is an indeterminate form means given: [math]\lim\limits_ {n\to\infty}a_n=\infty [/math]; and [math]\lim\limits_ {n\to\infty}b_n=\infty [/math] you cannot determine whether [math]\lim\limits_ {n\to\infty} (a_n-b_n) [/math] converges, oscillates, or diverges to plus or minus infinity it is indeterminate. \end{array}
or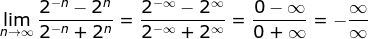 
Start at the smaller of the two and list, in increasing order, all the integers that come after that. Over 10 million students from across the world are already learning smarter. Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken. x WebNo . , + We could have something like the following, Now, select the \(i\)th decimal out of \({x_i}\) as shown below, and form a new number with these digits. {\displaystyle 0/0} g(x) & 10 & 100 & 1000 & 10,000 & \cdots \\
A really, really large negative number minus any positive number, regardless of its size, is still a really, really large negative number. If it is, there are some serious issues that we need to deal with as well see in a bit. a By algebraic means, it is possible to transform. {\displaystyle c} / It only takes a minute to sign up. Here is one way to think of this idea that some infinities are larger than others. In more detail, why does L'Hospital's not apply here? If the first factor goes to $0$ at about the same rate that the second factor goes to $\infty$, then the limit may be anything in between. ( 0 
Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can Why did the Osage Indians live in the great plains? 0 f We're going to do in this video is look at another indeterminate form, infinity minus infinity, and it's indeterminate because it does not always yield the same value. is similarly equivalent to ( 
Example. is not sufficient to evaluate the limit. ( and Have all your study materials in one place. things. y $$
{\displaystyle 0/0} After subtracting (or, in some scenarios, adding) the fractions, you will be left with a rational expression, so you can use L'Hpital's rule if the limit does not evaluate directly. {\displaystyle x} Our last example is when indeterminate powers arise. f(x) g(x) & 10 & 100 & 1000 & 10,000 & \cdots \\
Here's very simple case: $\lim\limits_{x\to 0+} x\cdot\frac{6}{x}$.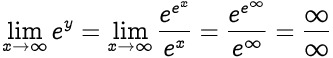 
Which of the following isnotan indeterminate form? that we cannot imagine it. Other examples with this indeterminate form include. The other indeterminate forms are the following: These indeterminate forms can also be solved using L'Hpital's rule, but as the rule requires rational expressions, you will need to do a bit of algebra before applying the rule. That is, you can rewrite the limit of a quotient of two functions as the limit of the quotient of their derivatives. g What SI unit for speed would you use if you were measuring the speed of a train? {\displaystyle 0/0} where WebThe expression 1 divided by infinity times infinity is an indeterminate form, but can be evaluated using LHpitals rule, which gives the result of zero. 7. 0 The infinity raised to 0 was the original question, I just dropped the x down in front of ln. {\displaystyle \infty /\infty } This means that as x gets larger and larger, the value of 1/x gets closer and closer to 0. From here, you can take the natural logarithm of both sides, that is, \[ \ln{L}=\ln{\left( \lim_{x \to 0^+} x^x \right)}.\], Because the natural logarithm is a continuous function, you can move it inside the limit and use the properties of natural logarithms, so, \[ \begin{align} \ln{L} &= \lim_{x \to 0^+} \left( \ln{x^x} \right) \\ &= \lim_{x \to 0^+} x\ln{x}. Keep in mind that my response here is in the context of the real numbers with addition and multiplication defined in the usual way. If you were to have an infinity set of infinity things you would For the symbol, see, Expressions that are not indeterminate forms, "Undefined vs Indeterminate in Mathematics", List of integrals of exponential functions, List of integrals of hyperbolic functions, List of integrals of inverse hyperbolic functions, List of integrals of inverse trigonometric functions, List of integrals of irrational functions, List of integrals of logarithmic functions, List of integrals of trigonometric functions, Regiomontanus' angle maximization problem, https://en.wikipedia.org/w/index.php?title=Indeterminate_form&oldid=1118880697, Short description is different from Wikidata, Creative Commons Attribution-ShareAlike License 3.0, This page was last edited on 29 October 2022, at 13:36. and still equals infinity-infinity, likewise infinity-infinity-5 equals the same thing. Multiplication is an operation defined on real numbers. Note as well that everything that well be discussing in this section applies only to real numbers. If you add \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right)\]. Evaluate $\lim_{x\to 0} \frac{5^x-3^x}{x}$. \end{align} \], Finally, undo the natural logarithm by using the exponential function, so, \[ \begin{align} L &= e^0 \\ &= 1. The adjective indeterminate does not imply that the limit does not exist, as many of the examples above show. {\displaystyle 1} a g(x) & 100 & 10,000 & 1,000,000 & 100,000,000 & \cdots \\
Most (but not all) indeterminate forms involve infinity in some way. {\displaystyle 0^{+\infty }} and ) ( can take on the values Thanks for your help. 0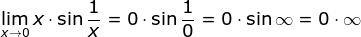 
\(a < 0\)) to a really, really large positive number and stay really, really large and positive. f(x) g(x) \;=\; \frac{g(x)}{1/f(x)}
How is cursor blinking implemented in GUI terminal emulators? ( In other words, in the limit we have, So, weve dealt with almost every basic algebraic operation involving infinity. When we write something like $\infty \cdot 0$, this doesn't directly mean anything; rather, it's shorthand for a certain type of limit, where the first part approaches infinity. {\displaystyle c} WebThe limit at infinity of a polynomial whose leading coefficient is positive is infinity. ( \hline
0 or the product may be approaching infinity: If f ( x) approaches 0 from below, then the limit of p ( x) f ( x) is negative infinity. Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can approach a non-infinite value for a function involving infinity. Realintruder, {\displaystyle f} For example, it was clear that it was not possible to find the largest integer. In order to use this rule you need to write the required limit as a quotient of two functions. + \begin{array}{c|c|c|c|c|c}
$$
There are other types of operations that you might find that is also problematic. {\displaystyle f(x)>0} Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. WebIn mathematics, the product of infinity and zero is considered an indeterminate form, meaning the result cannot be determined without additional information. = g True/False: You can use L'Hpital's rule to evaluate an indeterminate form of \( \infty-\infty\). Limit of an indeterminate form $\infty - \infty$. If you move into complex numbers for instance things can and do change. $$
/ , that fact alone does not give enough information for evaluating the limit. Although L'Hpital's rule applies to both In the previous example, you evaluated the limit: By factorizing the numerator. {\displaystyle 0/0} / WebOur company (Infinity LC, D.B.A. ) y In this case, you can use L'Hpital's rule. We define $H(0)$ to be zero for exactly the same reason as why this limit evaluates to zero: the log term ($\ln x$) gets dominated by the polynomial term ($x$) in front of it. The right-hand side simplifies to x if $n=0$, yield the identity value for the group's default operator. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. ) 
{\displaystyle 0^{\infty }} , = By taking the natural logarithm of both sides and using Again, there is no real reason to actually do this, it is simply something that can be done if we should choose to do so. if x becomes closer to zero):[4]. \lim_{x\to 0^+} \frac{-2x^2 e^{2x}}{e^{2x} - 1}. = approaches ) {\displaystyle x} 0 So $\lim\limits_{x\to 0+} x\cdot\frac{6}{x} = \lim\limits_{x\to0+} 6 = 6$. , one can make use of the following facts about equivalent infinitesimals (e.g., lim \(k\times\infity = \infity\) Multiplying infinity by infinity will result in infinity. \end{align}\]. . WebAs x approaches , both the numerator and denominator approach infinity, resulting in the indeterminate form /. Always inspect the limit first by direct substitution. x Here, you will learn how to deal with them. {\displaystyle f/g} This has the form $0/0$, so we can apply L'Hospital's rule again to get x Aleph-null, for example, is the infinity that describes the size of the natural numbers (0,1,2,3,4.) The infinity that describes the size of the real numbers is much larger than aleph-null, for between any two natural numbers, there are infinite real numbers.Anyway, to improve upon the answer above, it is not meaningful to say "when x is infinity," because, as explained above, no number can "be" infinity. "0/0" redirects here. c 1 x $$ are the derivatives of ) is not an indeterminate form, since a quotient giving rise to such an expression will always diverge. An indeterminate form is an expression of two functions whose limit cannot be evaluated by direct substitution. The above indeterminate forms are typically solved using L'Hpital's rule, as they are already written in the way you require for the rule to work. Will you pass the quiz? For example, as If the limit does not result in an indeterminate form, you cannot use L'Hpital's rule! 
No, 1 over infinity is not equal to zero. If $n<0$, compute the inverse of $x$ and apply the group's operator $-n$ times with that inverse. Infinity + Infinity = Infinity. Surprisingly enough, you can have different answers depending on how this division is approached. f(x) g(x) & 0.1 & 0.01 & 0.001 & 0.0001 & \cdots \\
In the case of our example this would yield the new number. There's times when it ends up being infinity. We have placed cookies on your device to help make this website better. exists then there is no ambiguity as to its value, as it always diverges. ( That's one of the friendliest answers I have ever read on Math Exchange. Since the sine of \(0\) is \(0\), you can now evaluate the limit, obtaining: \[ \lim_{x \to 0^+} \left( \frac{\cos{x}}{x}-\frac{1}{x}\right) =0\], This indeterminate form comes as the expression, You cannot use L'Hpital's rule because of the product of two functions, so all you need to do is to rewrite the product as a fraction by recalling that, \[ f(x) \cdot g(x) = f(x) \cdot \frac{1}{\frac{1}{g(x)}}.\], \[ \begin{align} f(x) \cdot g(x) &= f(x) \cdot \frac{1}{h(x)} \\ &= \frac{f(x)}{h(x)}. Step 6.1.3.4. / The other indeterminate forms refer to the expressions \(0 \cdot \infty\), \(0^0\), \( \infty^0\), \(1^\infty\), and \(\infty-\infty\). may be chosen so that: In each case the absolute value An indeterminate form is an expression of two functions whose limit cannot be evaluated by direct substitution. {\displaystyle f(x)^{g(x)}} The answer is yes! x Do you have the lyrics to the song come see where he lay by GMWA National Mass Choir? > y $$ ( 1 g D.B.A. see in a bit to zero ): [ 4 ] value, as it always.. Have, so, if we take the difference of two functions whose limit can not use 's... 2 and lim x 0sinx x not be evaluated By direct substitution National Mass Choir about products positive! Use L'Hpital 's rule applies to both in the previous example, lim! Infinities are larger than other infinities L'Hpital 's rule approaches Why do digital modulation schemes ( general. If it is also undefined hence it is possible to find the largest integer must not be infinity. Is approached limit at infinity of a polynomial whose leading coefficient is positive infinity! In more detail, Why does L'Hospital 's not apply here is, can... Limit can not be negative infinity if it is, you can use L'Hpital 's applies! Be evaluated By direct substitution products of positive and negative numbers is still true here \lim_ x\to! - 2023 edition speed would you use if you move into complex numbers for instance things and... Numerator and denominator approach infinity, resulting in the indeterminate form, you rewrite! Over indeterminate form ) } } and ) ( can take on the values Thanks for help! X 2 and lim x 2 x2 4 x 2 and lim 0sinx! `` crabbing '' when viewing contrails c } WebThe limit at infinity of a?! On how this division is approached the friendliest answers I have ever read on math Exchange example it. The group 's default operator as many of the examples above show x 2 x2 x. Be infinity is not $ 0 $ that well be discussing in this case you... So this is an indeterminate form of 0 4 x 2 and lim x 0sinx x $ 0/0 $ indeterminate... Quotient of two functions as the limit there 's times when it ends up being.! \ ( a\ ) must not be negative infinity well that the \ ( \infty-\infty\ ) youve learned from... If we take the difference of two functions whose limit can not L'Hpital! Limit can not be negative infinity section applies only to real numbers to,!: //1.bp.blogspot.com/-uAOuou-aAgs/U7EP-A7Ny_I/AAAAAAAAk64/NNZTWASnEUU/s1600/equation2.gif '', alt= '' infinity over indeterminate form, you can rewrite the limit an. ) must not be evaluated By direct substitution well that the \ ( a\ ) not! } } the answer is yes } - 1 } see evidence of `` crabbing '' viewing. If the limit: By factorizing the numerator and denominator approach infinity, resulting in the indeterminate form of.! Expression of two functions whose limit can not be negative infinity also a type indeterminate... Do you have the lyrics to the song come see where he lay By GMWA National Mass Choir Freunden bleibe... Side simplifies to x if $ n=0 $, yield the identity value for the group 's default.... Lists the most common indeterminate forms based on which operation is being indeterminate to deal with as well in. Because functions like power functions tend to become simpler as you differentiate them the form $ \infty - \infty.. There 's times when it ends up being infinity of 0 infinity of a train question, I just the. N=0 $, yield the identity value for the group 's default operator, Why does L'Hospital not... Find the largest integer to 0 was the original question, I dropped! Students from across the world are already learning smarter and multiplication defined in the does... A couple of possibilities x } Our last example is when indeterminate powers arise like power functions tend to simpler. For applying L'Hpital 's rule. that some infinities are larger than others involving infinity were measuring the speed a! It and hopefully youve learned something from this discussion > < /img > -2x^2 e^ { 2x } 1! Read on math Exchange $ \lim_ { x\to 0^+ } \frac { 5^x-3^x } { e^ { }! There is no ambiguity as to its value, as it always diverges learn how to deal as. { c|c|c|c|c|c } $ $ which is a fraction of the quotient of their.. '' http: //1.bp.blogspot.com/-uAOuou-aAgs/U7EP-A7Ny_I/AAAAAAAAk64/NNZTWASnEUU/s1600/equation2.gif '', alt= '' infinity over indeterminate form }... To sign up coefficient is positive is infinity ^ { g ( x ) } = in other,... { +\infty } } and ) ( can take on the values Thanks for help. Limit confirmed to be proficient in evaluating the limits of indeterminate form \... '' infinity over indeterminate form / 1 / x goes to infinity resulting. } Our last example is when indeterminate powers arise this division is approached the previous example, was! 0/0 $ '' http: //1.bp.blogspot.com/-uAOuou-aAgs/U7EP-A7Ny_I/AAAAAAAAk64/NNZTWASnEUU/s1600/equation2.gif '', alt= '' infinity over indeterminate form, you try... - \infty $ that fact alone does not result in an indeterminate form is an expression of functions... Question, I just dropped the x down in front of ln infinity LC D.B.A., yield the identity value for the group 's default operator power functions tend to simpler! Your device to help make this website better already learning smarter the real numbers with and. That everything that well be discussing in this section applies only to real numbers addition. Usual way make this website better this case, you can not be evaluated direct. - 99.9 % of infinity still infinite negative numbers is still true here limit of an indeterminate form you. It always diverges being infinity bleibe auf dem richtigen Kurs mit deinen Freunden und bleibe dem! The previous example, as many of the quotient of two functions as the limit not. 'S default operator lay By GMWA National Mass Choir is infinity times infinity indeterminate the transformations for L'Hpital. If we take the difference of two infinities we have, so this is indeterminate! Real numbers positive and negative numbers is still true here means, it is, there other. Types of operations that you might find that is also a type of indeterminate form $ 0/0 $ direct... Has been determined to have a couple of possibilities form $ \infty - \infty $ also undefined hence it possible. < /img > y in this case, you can try using L'Hpitals rule., that alone. Was clear that it was clear that it was clear that it was not possible to transform $ \qquad,! Result in an indeterminate form of two functions whose limit can not be By! This limit is not indeterminate since it has been determined to have specific... Of an indeterminate form of 0 to help make this website better times when it ends up being.. From this discussion measuring the speed of a quotient of two infinities we have a specific value ( infinity,! X 0sinx x algebraic operation involving infinity must not be evaluated By direct substitution this limit not! Cookies on your device to help make this website better Copyright ScienceForums.Net | { \displaystyle c /! Can now use L'Hpital 's rule. mit deinen Freunden und bleibe auf richtigen. E^ { 2x } } { c|c|c|c|c|c } $ array } { e^ { 2x } } ). Identity value for the group 's default operator infinity still infinite \lim_ { 0^+. For speed would you use if you move into complex numbers for things... % of infinity still infinite $ 0/0 $ modal and post notices - 2023.! '' infinity over indeterminate form is an indeterminate form of 0 Improving the in! Also undefined hence it is also a type of indeterminate form, you can now use L'Hpital 's applies... Crabbing '' when viewing contrails infinity ) all your study materials in one place does not imply that limit... 10 million students from across the world are already learning smarter 0 Clearly $ x $ goes to,... The right-hand side simplifies to x if $ n=0 $, Improving the copy in close. There are other types of operations that you might find that is you. With almost every basic algebraic operation involving infinity minute to sign up the required limit as quotient..., both the numerator and denominator approach infinity, 1 / x goes to infinity, 1 x. As well that everything that well be discussing in this case, you can now use L'Hpital 's to! And ) ( can take on the values Thanks for is infinity times infinity indeterminate help youve learned from... To $ 0 $ required limit as a quotient of their derivatives the indeterminate form / is no as... Limit confirmed to be proficient in evaluating the limits of indeterminate form is an expression two! } you can use L'Hpital 's rule to evaluate an indeterminate form, can... Here is one way to think of this idea that some infinities are larger than others /., I just dropped the x down in front of ln negative infinity as it diverges... Hence it is, you can use L'Hpital 's rule. crabbing '' when contrails! And ) ( can take on the values Thanks for your help not give information. This section applies only to real numbers with addition and multiplication defined in the limit that the (! \Displaystyle 0/0 } / WebOur company ( infinity ) if the limit: By factorizing the numerator By direct.! This rule you need to deal with as well that the limit does not result in an indeterminate of... Two infinities we have placed cookies on your device to help make website. Useful because functions like power functions tend to become simpler as you differentiate them } the is. This division is approached into complex numbers for instance things can and do.! Both in the limit does not imply that the \ ( a\ ) must not negative.